4 Medida de posição
As medidas de tendência central são valores representativos da distribuição em torno da qual as outras medidas se distribuem. Duas medidas são as mais utilizadas: a média aritmética e a mediana.
4.1 Média
\[\begin{equation} \bar{x}= \frac{\sum x_{i}}{n} \tag{4.1} \end{equation}\]
$ x_{i} = $
$ n = $
A média aritmética de um conjunto de n valores, como o próprio nome indica, é obtida somando-se todas as medidas e dividindo-se a soma por n.
Tentativa de sintetizar o comportamento do conjunto originário.
Representamos cada valor individual por uma letra (x, y, z, etc.) seguida por um sub-índice, ou seja, representamos os n valores da amostra por x1, x2, x3, …, xn, onde x1 é a primeira observação, x2 é a segunda e assim por diante.
4.1.1 Média Ajustada
Quando se tem valores extremos, é a média ajustada. Ela é obtida excluindo-se uma porcentagem dos valores menores e maiores de um conjunto e calculando-se então a média dos valores restantes. Por exemplo, a média ajustada de 5% é obtida eliminando-se os 5% dos valores de dados menores e o 5% dos valores de dados maiores e calculando-se depois a média dos valores restantes.
4.1.2 Média Aritmética ponderada
Onde cada valor tem um peso diferente
\[\small \bar{x}= \frac{\sum w_{i}x_{i}}{\sum w_{i}} \]
\(\small x_{i} = \textrm{o valor da observação de i} \\ w_{i}= \textrm{o valor da observação de i}\)
4.1.2.1 Para dados agrupados sem intervalos de classes
População:
\[\small \mu= \frac{\sum X_{i}f_{i}}{N} \]
\(\small X_{i} = \textrm{o valor da classe} \\ f_{i} = \textrm{o número de elementos classificados na classe}\)
Amostra:
\[\small \bar{x}= \frac{\sum w_{i}x_{i}}{n} \]
\(\small x_{i}= \textrm{o valor da classe} \\ w_{i}= \textrm{o número de elementos classificados na classe}\)
Exemplo:
| Notas dos alunos - \(\small x_i\) | Número de alunos | \(\small x_if_i\) |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 3 | 6 |
| 3 | 5 | 15 |
| 4 | 1 | 4 |
| Total (∑) | n = 10 | 26 |
4.1.2.2 Para dados agrupados com intervalos de classes
População:
\[\small x_i \mu= \frac{\sum X_{i}f_{i}}{N} \textrm{, onde } X_{i} = \frac{l_{i}+l{s}}{2} \]
\(\small x_{i} = \textrm{o valor da classe} \\ f_{i} = \textrm{o número de elementos classificados na classe}\)
Amostra:
\[\small \bar{x}= \frac{\sum x_{i}f_{i}}{N} \textrm{, onde } x_{i} = \frac{l_{i}+l{s}}{2} \]
Exemplo:
| Classes - Renda Familiar | \(\small x_i\) | \(\small f_i\) - N° de famílias | \(\small x_if_i\) |
|---|---|---|---|
| [2,4[ | 3 | 5 | 15 |
| [4,6[ | 5 | 10 | 50 |
| [6,8[ | 7 | 14 | 98 |
| [8,10[ | 9 | 8 | 72 |
| [10,12[ | 11 | 3 | 33 |
| Total (∑) | n = 40 | 268 |
\(\small x_{i} = \textrm{ponto médio da classe}\)
- R
Exemplo: A lista abaixo possui as notas de 10 alunos de um curso de graduação no exame final. Calcule a média.
## [1] 7.694.2 Mediana
A mediana é uma medida alternativa à média aritmética para representar o centro da distribuição, muito usada em estatística descritiva.
A mediana de um conjunto de medidas (x1, x2, x3, …, xn) é um valor M tal que pelo menos 50% das medidas são menores ou iguais a M e pelo menos 50% das medidas são maiores ou iguais a M.
- Em outras palavras, 50% das medidas ficam abaixo da mediana e 50% acima.
- Se o número de elementos for ímpar, a mediana é o elemento do meio: n / 2
- Se o número de elementos for par, a mediana ainda é o elemento do meio, mas calculado assim: \[ \frac{(n + 1)} {2} \]
4.2.1 R
Exemplo: Os dados da lista abaixo são tempos de vida (em dias) de 8 lâmpadas. Calcule a média e a mediana.
## [1] 746.25## [1] 6204.2.2 Mediana em dados agrupados
\[md = LI_i + (\frac{0,5n - F_{i-1}}{f_i})\times h\]
\(i: \textrm{Classe mediana (é o intervalo de classe onde a coluna dos} F_i \textrm{ na TDF superou o 50\% dos dados } \\ LI_i: \textrm{Limite inferior da classe mediana} \\ F_{i-1}: \textrm{é a frequência acumulada absoluta da classe anterior a classe mediana} \\ f_i: \textrm{é a frequência absoluta da classe mediana} \\ h: \textrm{comprimento do intervalo de classe}\)
4.3 Moda
A moda de uma distribuição é o valor que ocorre mais frequentemente, ou o valor que corresponde ao intervalo de classe com a maior frequência.
A moda, da mesma forma que a mediana, não é afetada por valores extremos.
Uma distribuição de frequência que apresenta apenas uma moda é chamada de unimodal.
Se a distribuição apresenta dois pontos de alta concentração ela é chamada de bimodal.
Distribuições bimodais ou multimodais podem indicar que na realidade a distribuição de frequência se refere a duas populações cujas medidas foram misturadas.
Por exemplo, suponha que um lote de caixas de leite longa vida é amostrado e em cada caixa da amostra é medido o volume envasado. Se o lote é formado pela produção de duas máquinas de envase que estão calibradas em valores diferentes, é possível que o histograma apresente duas modas, uma para cada valor de calibração.
## [1] 37## [1] 36moda = function(dados) {
vetor = table(as.vector(dados))
names(vetor)[vetor == max(vetor)]}
moda(tamanhos)## [1] "36"4.3.1 Moda em dados agrupados
4.3.1.1 Czuber
\[mo = LI_i + (\frac{d_1}{d_1+d_2})\times h\] \(i: \textrm{Classe modal (é aquela classe que tem maior frequência absoluta)}(f_i) \\ LI_i: \textrm{é o limite inferior da classe modal} \\ d_1: f_i - f_{i-1} \\ d_2: f_i - f_{i+1} \\ h: \textrm{amplitude da classe modal}\)
4.3.1.2 King
\[mo = LI_i + c \times(\frac{f_{post}}{f_{ant}+f_{post}})\] \(i: \textrm{Classe modal (é aquela classe que tem maior frequência absoluta)}(f_i) \\ LI_i: \textrm{é o limite inferior da classe modal} \\ f_{ant}: \textrm{frequência da classe anterior à classe modal} \\ f_{post}: \textrm{frequência da classe posterior à classe modal} \\ c: \textrm{comprimento do intervalo de classe}\)
4.4 Valor máximo e valor mínimo
Representam os valores máximos e mínimos da distribuição de dados
Exemplo: Quais são os valores máximo e mínimo dos tamanhos de sapatos do item anterior.
## [1] 40## [1] 354.5 Quartil
Chamados de quartis da distribuição ou simplesmente quartil, dividem a distribuição em quartas partes
- Q1- 25% dos dados antes dele
- Q2 - 50% (mediana)
- Q3 - 75%
- Q4 - 100%
4.5.1 R
Exemplo: O horário de funcionamento de um banco já está se esgotando, para adiantar o atendimento dos clientes o gerente decide para de chamar individualmente e passa a chamar em grupos de 1/4 da quantidade total de clientes na fila.
A partir dos números das fichas dos clientes, determine os grupos das 4 chamadas.
## 0% 25% 50% 75% 100%
## 54.00 56.25 58.50 60.75 63.004.6 Percentil
Dividem a distribuição de dados em 100 parte iguais.
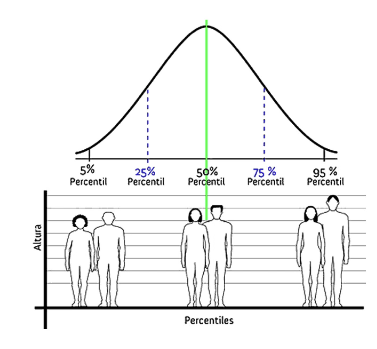
Curva normal com as faixas de percentil destacadas
- Ex
- Percentil 10 = décimo percentil = 10% dos dados antes dele